word-search-ii

< Previous 　　　　　　　　　　　　　　　　 Next >

212. Word Search II (Hard)

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

 

Example 1:

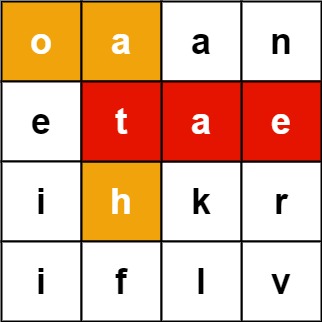
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

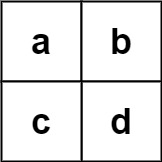
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

 

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 12
• board[i][j] is a lowercase English letter.
• 1 <= words.length <= 3 * 104
• 1 <= words[i].length <= 10
• words[i] consists of lowercase English letters.
• All the strings of words are unique.

Related Topics

[Array] [String] [Backtracking] [Trie] [Matrix]

Similar Questions

1. Word Search (Medium)
2. Unique Paths III (Hard)

Hints

Hint 1

You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier?

Hint 2

If the current candidate does not exist in all words' prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie? If you would like to learn how to implement a basic trie, please work on this problem: Implement Trie (Prefix Tree) first.