valid-mountain-array.md

Valid Mountain Array

{% hint style="info" %} https://leetcode.com/problems/valid-mountain-array/solution/ {% endhint %}

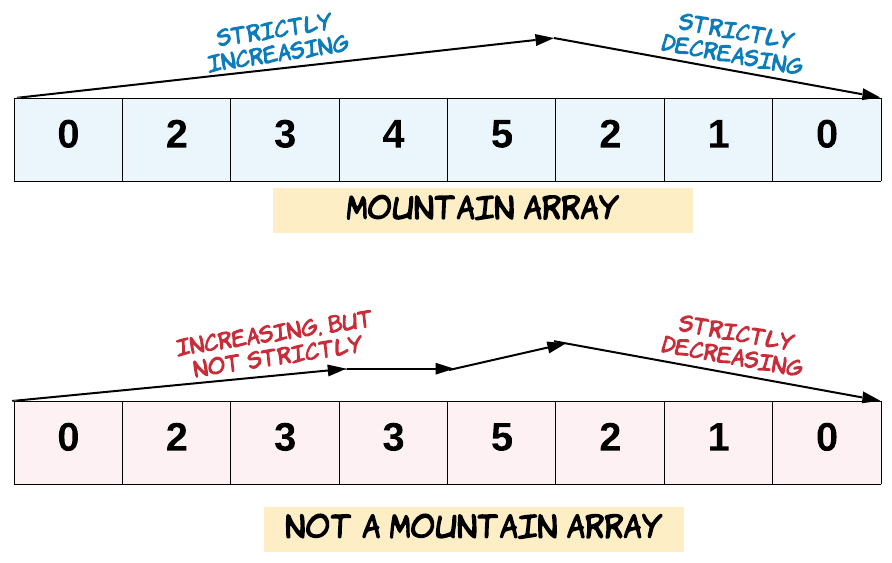
{% tabs %} {% tab title="Question" %} Given an array of integers arr, return true if and only if it is a valid mountain array.

Recall that arr is a mountain array if and only if:

• arr.length >= 3
• There exists some i with 0 < i < arr.length - 1 such that:
  • arr[0] < arr[1] < ... < arr[i - 1] < A[i]
  • arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

Example 1:

Input: arr = [2,1]
Output: false

{% endtab %}

{% tab title="Answer" %} From the Leetcode solution:

Intuition

If we walk along the mountain from left to right, we have to move strictly up, then strictly down.

Algorithm

Let's walk up from left to right until we can't: that has to be the peak. We should ensure the peak is not the first or last element. Then, we walk down. If we reach the end, the array is valid, otherwise its not.

class Solution(object):
    def validMountainArray(self, A):
        N = len(A)
        i = 0

        # walk up
        while i+1 < N and A[i] < A[i+1]:
            i += 1

        # peak can't be first or last
        if i == 0 or i == N-1:
            return False

        # walk down
        while i+1 < N and A[i] > A[i+1]:
            i += 1

        return i == N-1

From here

Two people climb from left and from right separately. If they are climbing the same mountain, they will meet at the same point.

class Solution:
    def validMountainArray(self, arr: List[int]) -> bool:
        A = arr
        i, j, n = 0, len(A) - 1, len(A)
        while i + 1 < n and A[i] < A[i + 1]: 
            i += 1
        while j > 0 and A[j - 1] > A[j]: 
            j -= 1
        return 0 < i == j < n - 1

{% endtab %} {% endtabs %}