Skip to content

Latest commit

 

History

History
91 lines (62 loc) · 4.43 KB

README.md

File metadata and controls

91 lines (62 loc) · 4.43 KB
Raw

Link prediction with supervised random walks

A Matlab implementation of the supervised random walks algorithm for link prediction proposed by Backstrom and Leskovec.

For detailed explanation of the algorithm we refer users to the their 2011 paper.

User manual

You can test the code with artificial data to check its performance and computational efficiency. To do this you need to generate a random dataset with some prespecified parameters. Next you can use a parameter learner and see how well it will guess the parameters you specified in the previous step.

%generate a random dataset, if you want to change the number of instances,
%features or the weighter function, simply change the respective properties 
%of the generator before invoking the generate function

generator = random_generators.RandomInstancesGenerator();
[dataset,weighter,alpha,true_w] = generator.generate();

%use a WMW cost function; a time limit of 30 seconds and progress printing
%for learning the parameters
learner = utils.ParameterLearner(weighter,alpha,utils.CostFunction(),30,true);
learned_w = learner.learn(dataset);

disp(['The true parameters are: ',num2str(true_w)])
disp(['The learned parameters are: ',num2str(learned_w)])

The above code is pretty self-explanatory, but I feel it is important to discuss the system abstractions here. I designed the system guided by the Weka organization, so anyone who is familiar with it will feel very comfortable using this framework. I'll just give a brief definition of the major abstractions.

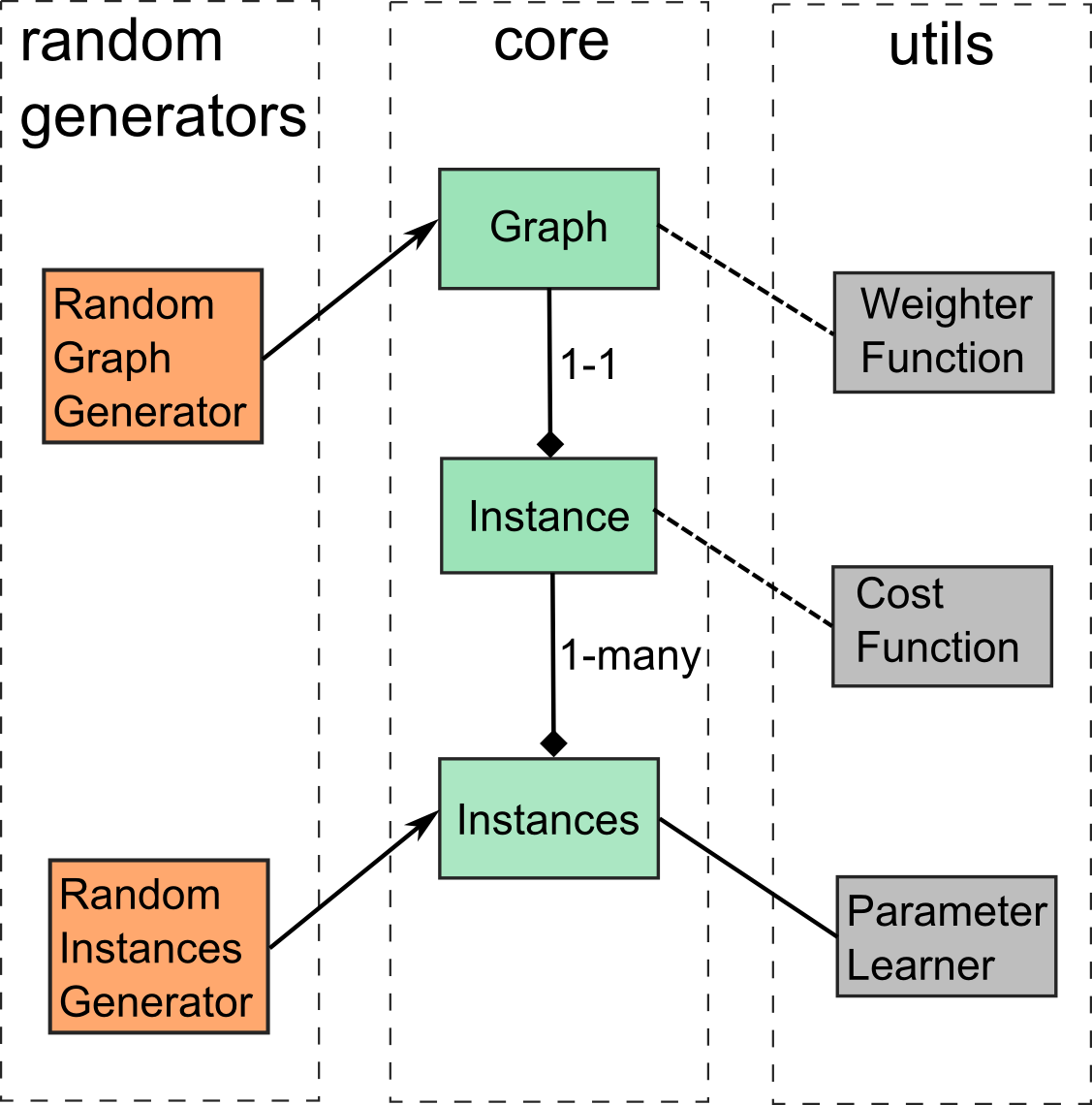
  • A Graph is represented by an unweighted adjacency matrix that determines which nodes are connected to each other. Additionally, each edge has an array of values attached to it which we call features.

  • An Instance object defines the positive and negative links for a given node. You can think of these as the classes/labels for the node in a multilabel classification task, which ultimately is what we are trying to learn to predict. For predicting the positive and negative links the algorithm uses information about the graph topology and the features for each link. The effect that each feature has on the prediction depends heavily on the feature parameters and slightly on the weighter function.

  • In order to learn anything useful, the algorithm needs many instance objects which are grouped in an Instances object for easier manipulation.

  • The ParameterLearner tries to find those parameters that give the predictions that match the positive/negative links specified. Each instance is treated independently although some of them may share the same graph. The learner uses the cost function to evaluate its predictions.

The system architecture and package structure is summarized in the following diagram

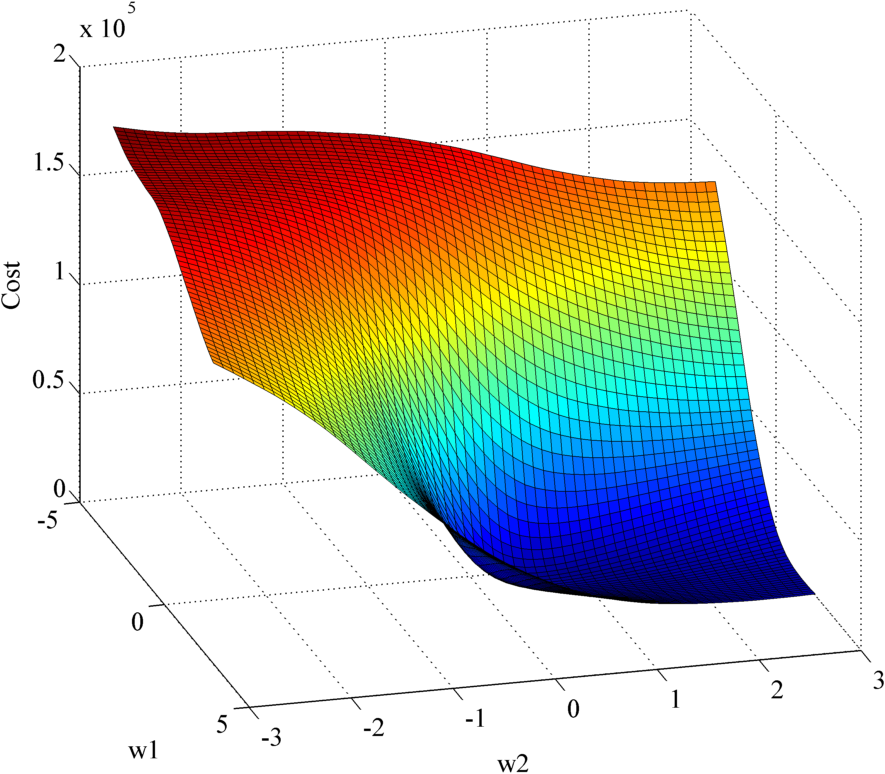
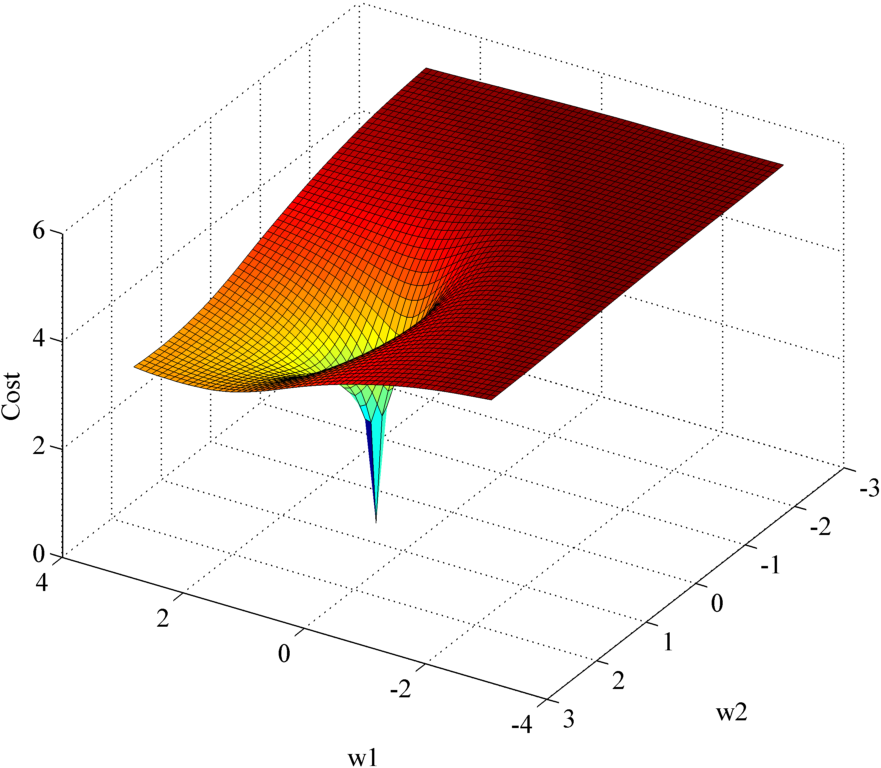
alt tag

You can confirm that the problem is smooth by plotting the cost function for a small number of features using the following code

%define the bounds and the granularity
granularity = 10;
bound1 = 2.5;
bound2 = 2.5;
costf = utils.CostFunction();

%create the meshgrid and initilize the cost
x = -bound1:bound1/granularity*2:bound1;
y = -bound2:bound2/granularity*2:bound2;
[X,Y] = meshgrid(x,y);
n = length(x);
Z = zeros(n,n);

%generate the random dataset
generator = random_generators.RandomInstancesGenerator();
[dataset,weighter,alpha,true_w] = generator.generate();

%calculate the cost for each point
parfor i=1:n
    for k=1:n
        cost = dataset.calcCost(weighter,alpha,costf,[X(i,k)+0.000001,Y(i,k)+0.000001]);
        Z(i,k) = cost;
    end
end

%plot the results
figure;surf(X,Y,Z);xlabel('w1');ylabel('w2');title('cost');
figure;surf(X,Y,log(Z));xlabel('w1');ylabel('w2');title('log cost');

By increasing the granularity you can get the following images

alt tag

alt tag

I implemented this mostly to hone my Matlab skills. However, I also did another implementation, this time in Java, which I am currently using to study the social network landscape in Macedonia.