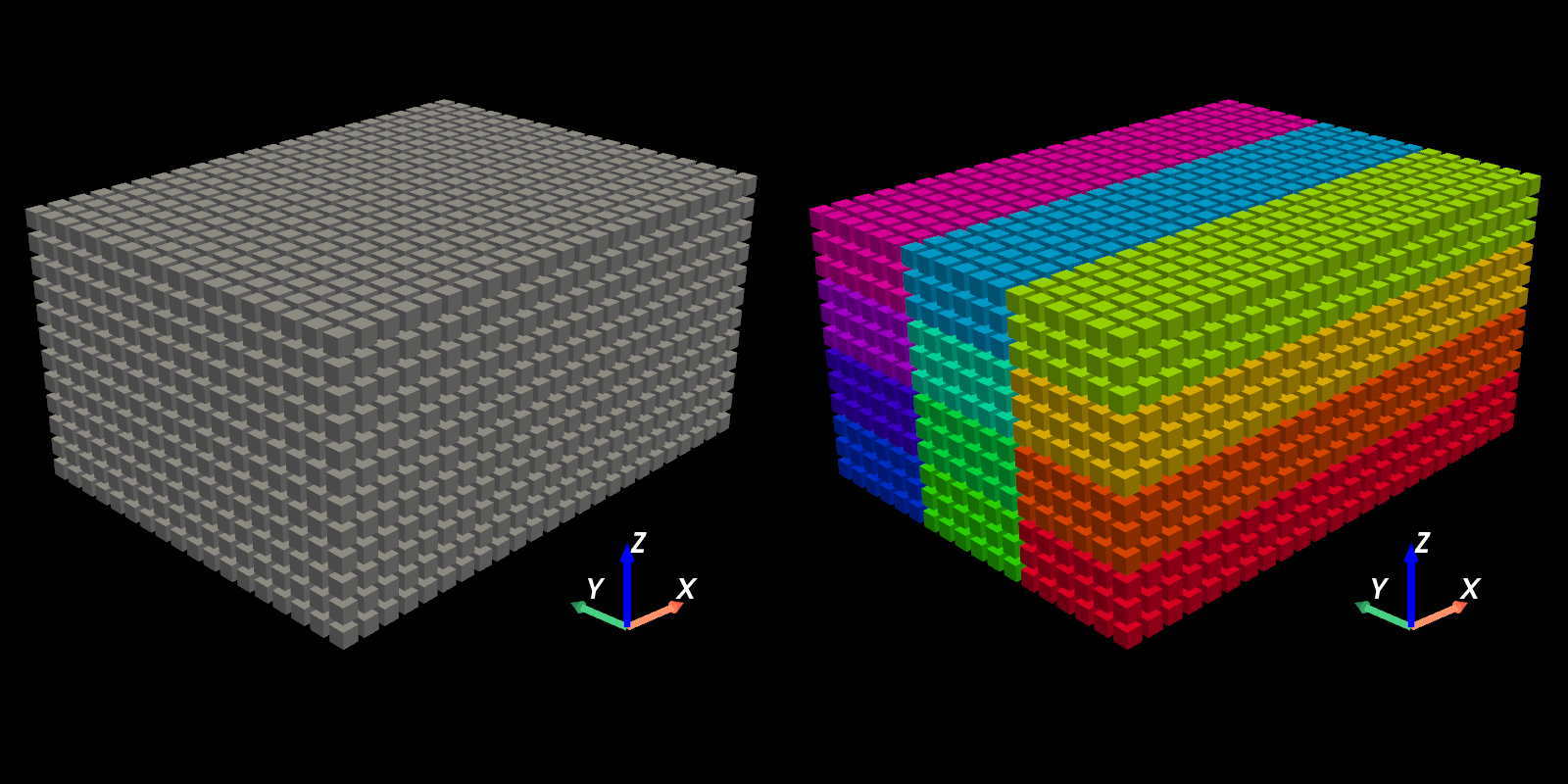
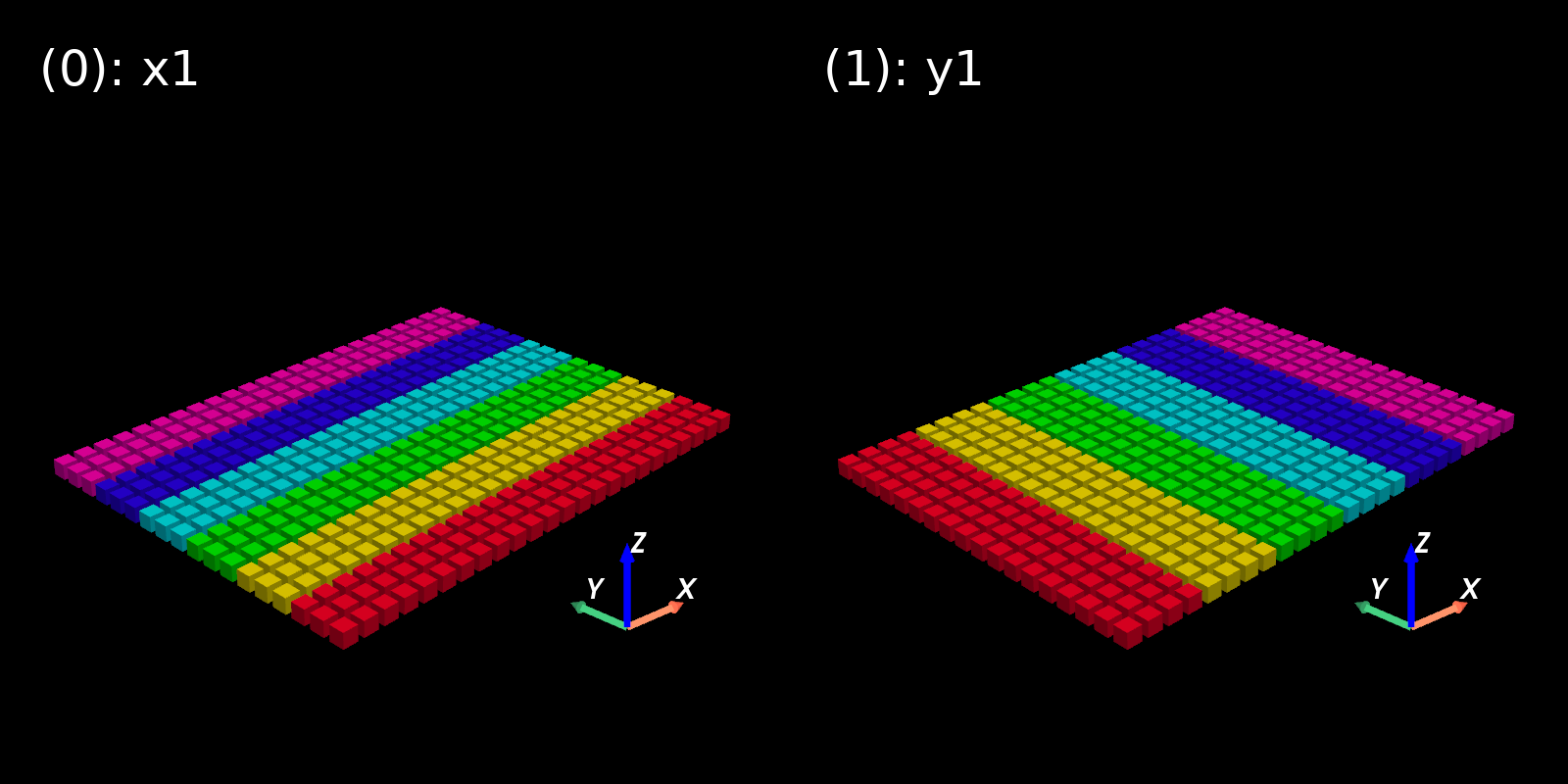
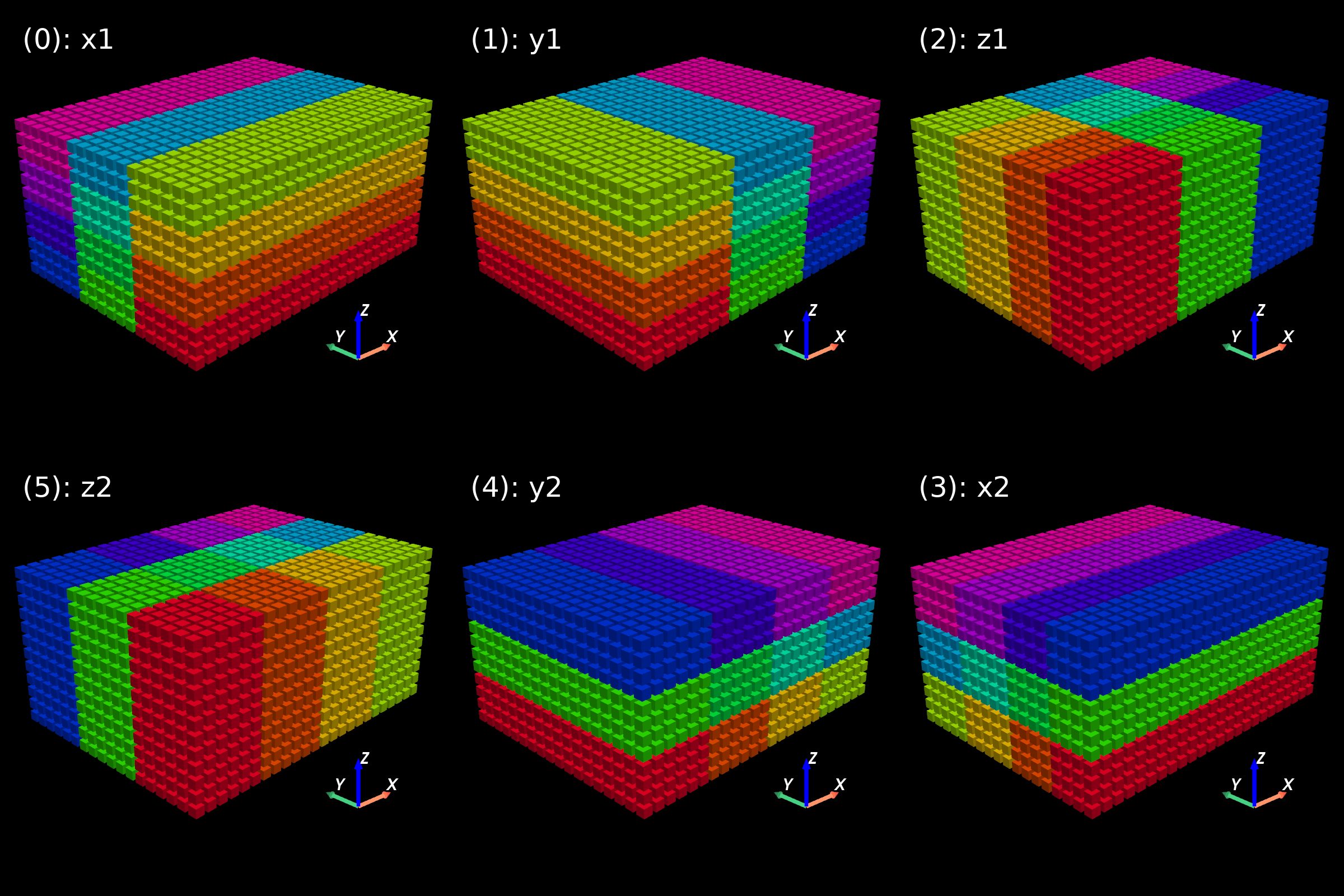
This library decomposes two- and three-dimensional structured meshes between multiple processes in a pencil-like manner:
The main objective is to perform so-called parallel matrix transpose (rotating pencils):
which are useful for performing operations where a process needs to contain all data in one direction, e.g. multi-dimensional Fast Fourier Transforms or Thomas algorithm.
C99-compatible.- Domain decompositions and pencil rotations for arbitrary data types using a single function.
- Memory efficient: no internal buffers to store intermediate data.
- Matrix transposition (row-major and column-major orders are interchanged) while rotating the pencils to improve the cache efficiency of the successive operations (e.g. Fast Fourier Transforms, Thomas algorithm).
- Transparent (i.e. hackable) and well-documented implementation.
- Well-tested for various data types, domain sizes and number of processes.
Checkout this project
git clone https://github.com/NaokiHori/SimpleDecomp
cd SimpleDecompand execute
make all
mpirun -2 --oversubscribe ./a.outwhich runs a small program to get started, which is elaborated below.
To understand the concept easily, I consider a two-dimensional array which is split into two sub-arrays (i.e. two processes) and is contained by each process:
+-------------+
| 16 17 18 19 |
| 12 13 14 15 |
| 08 09 10 11 |
+-------------+
| 04 05 06 07 |
| 00 01 02 03 |
+-------------+
where the lower (from 00 to 07) and the upper (from 08 to 19) parts are stored by the rank 0 and 1, respectively. Notice that the matrix is stored in the row-major order, i.e.
00 01 02 03 04 05 06 07
in the buffer of the rank 0, and
08 09 10 11 12 13 14 15 16 17 18 19
in the buffer of the rank 1.
They are called x pencils in this project.
After the pencils are rotated, I obtain
+-------+-------+
| 16 17 | 18 19 |
| 12 13 | 14 15 |
| 08 09 | 10 11 |
| 04 05 | 06 07 |
| 00 01 | 02 03 |
+-------+-------+
where the left and the right parts are stored by the rank 0 and 1, respectively. Notice that the matrix is now stored in the column-major order, i.e.:
00 04 08 12 16 01 05 09 13 17
in the buffer of the rank 0, while
02 06 10 14 18 03 07 11 15 19
in the buffer of the rank 1.
They are named as y pencils in this project.
Check src/main.c to see how the matrix is initialised and the library APIs are called.
Please refer to the documentation for practical usages and all available APIs.
I use this library to solve the incompressible Navier-Stokes equations efficiently on clusters.
Although the concept is similar to 2decomp-fft, the pencil rotations are largely tailored to my purposes and the implementation is simplified.
I also recognise many other nice libraries which aim to do the same thing (in Juila or in Fortran, I am pretty sure there are more).
This library is inspired by 2decomp-fft.