[TOC]
| 数据结构 | 相关 |
|---|---|
| 顺序线性表:向量 Vector | |
| 单链表 Singly Linked List | 1. 双向链表 Double Linked Lists 2. 静态链表 Static List 3. 对称矩阵 Symmetric Matrix 4. 稀疏矩阵 Sparse Matrix |
| 哈希表 Hash Table | 1. 散列函数 Hash Function 2. 解决碰撞/填充因子 Collision Resolution |
| 栈和队列 Stack & Queue | 1. 广义表 Generalized List/GList 2. 双端队列 Deque |
| 队列 Queue | 1. 链表实现 Linked List Implementation 2. 循环数组实现 ArrayQueue 3. 双端队列 Deque 4. 优先队列 Priority Queue 5. 循环队列 Circular Queue |
| 字符串 String | 1. KMP 算法 2. 有限状态自动机 3. 模式匹配有限状态自动机 4. BM 模式匹配算法 5. BM-KMP 算法 6. BF 算法 |
| 树 Tree | 1. 二叉树 Binary Tree 2. 并查集 Union-Find 3. Huffman 树 |
| 数组实现的堆 Heap | 1. 极大堆和极小堆 Max Heap and Min Heap 2. 极大极小堆 3. 双端堆 Deap 4. d 叉堆 |
| 树实现的堆 Heap | 1. 左堆 Leftist Tree/Leftist Heap 2. 扁堆 3. 二项式堆 4. 斐波那契堆 Fibonacco Heap 5. 配对堆 Pairing Heap |
| 查找 Search | 1. 哈希表 Hash 2. 跳跃表 Skip List 3. 排序二叉树 Binary Sort Tree 4. AVL 树 5. B 树 / B+ 树 / B* 树 6. AA 树 7. 红黑树 Red Black Tree 8. 排序二叉堆 Binary Heap 9. Splay 树 10. 双链树 Double Chained Tree 11. Trie 树 12. R 树 |
| ——————————————– | ——————————————————————————————– |
| 算法 | 具体类型 | 相关 |
|---|---|---|
| 排序算法 | 1. 冒泡排序 2. 插入排序 3. 选择排序 4. 希尔 Shell 排序 5. 快速排序 6. 归并排序 7. 堆排序 8. 线性排序算法 9. 自省排序 10. 间接排序 11. 计数排序 12. 基数排序 13. 桶排序 14. 外部排序 - k 路归并败者树 15. 外部排序 - 最佳归并树 | |
| 递归与分治 | 1. 二分搜索/查找 2. 大整数的乘法 3. Strassen 矩阵乘法 4. 棋盘覆盖 5. 合并排序 6. 快速排序 7. 线性时间选择 8. 最接近点对问题 9. 循环赛日程表 | |
| 动态规划 | 1. 矩阵连乘问题 2. 最长公共子序列 3. 最大子段和 4. 凸多边形最优三角剖分 5. 多边形游戏 6. 图像压缩 7. 电路布线 8. 流水作业调度 9. 0-1 背包问题/背包九讲 10. 最优二叉搜索树 11. 动态规划加速原理 12. 树型 DP | |
| 贪心 | 1. 活动安排问题 2. 最优装载 3. 哈夫曼编码 4. 单源最短路径 5. 最小生成树 6. 多机调度问题 | |
| 回溯法 | 1. 装载问题 2. 批处理作业调度 3. 符号三角形问题 4. n 后问题 5. 0-1 背包问题 6. 最大团问题 7. 图的 m 着色问题 8. 旅行售货员问题 9. 圆排列问题 10. 电路板排列问题 11. 连续邮资问题 | |
| 搜索 | 1. 枚举 2. DFS 3. BFS 4. 启发式搜索 | |
| 随机化 | 1. 随机数 2. 数值随机化算法 3. Sherwood 舍伍德算法 4. Las Vegas 拉斯维加斯算法 5. Monte Carlo 蒙特卡罗算法 | 1. 计算 π 值 2. 计算定积分 3. 解非线性方程组 4. 线性时间选择算法 5. 跳跃表 6. n 后问题 7. 整数因子分解 8. 主元素问题 9. 素数测试 |
| 图论 | 1. 遍历 DFS / BFS 2. AOV / AOE 网络 3. Kruskal 算法(最小生成树) 4. Prim 算法(最小生成树) 5. Boruvka 算法(最小生成树) 6. Dijkstra 算法(单源最短路径) 7. Bellman-Ford 算法(单源最短路径) 8. SPFA 算法(单源最短路径) 9. Floyd 算法(多源最短路径) 10. Johnson 算法(多源最短路径) 11. Fleury 算法(欧拉回路) 12. Ford-Fulkerson 算法(最大网络流增广路) 13. Edmonds-Karp 算法(最大网络流) 14. Dinic 算法(最大网络流) 15. 一般预流推进算法 16. 最高标号预流推进 HLPP 算法 17. Primal-Dual 原始对偶算法(最小费用流)18. Kosaraju 算法(有向图强连通分量) 19. Tarjan 算法(有向图强连通分量) 20. Gabow 算法(有向图强连通分量) 21. 匈牙利算法(二分图匹配) 22. Hopcroft-Karp 算法(二分图匹配) 23. kuhn munkras 算法(二分图最佳匹配) 24. Edmonds’ Blossom-Contraction 算法(一般图匹配) | 1. 图遍历 2. 有向图和无向图的强弱连通性 3. 割点/割边 3. AOV 网络和拓扑排序 4. AOE 网络和关键路径 5. 最小代价生成树/次小生成树 6. 最短路径问题/第 K 短路问题 7. 最大网络流问题 8. 最小费用流问题 9. 图着色问题 10. 差分约束系统 11. 欧拉回路 12. 中国邮递员问题 13. 汉密尔顿回路 14. 最佳边割集/最佳点割集/最小边割集/最小点割集/最小路径覆盖/最小点集覆盖 15. 边覆盖集 16. 二分图完美匹配和最大匹配问题 17. 仙人掌图 18. 弦图 19. 稳定婚姻问题 20. 最大团问题 |
| 数论 | 1. 最大公约数 2. 最小公倍数 3. 分解质因数 4. 素数判定 5. 进制转换 6. 高精度计算 7. 整除问题 8. 同余问题 9. 欧拉函数 10. 扩展欧几里得 11. 置换群 12. 母函数 13. 离散变换 14. 康托展开 15. 矩阵 16. 向量 17. 线性方程组 18. 线性规划 | |
| 几何 | 1. 凸包 - Gift wrapping 2. 凸包 - Graham scan 3. 线段问题 4. 多边形和多面体相关问题 | |
| NP 完全 | 1. 计算模型 2. P 类与 NP 类问题 3. NP 完全问题 4. NP 完全问题的近似算法 | 1. 随机存取机 RAM 2. 随机存取存储程序机 RASP 3. 图灵机 4. 非确定性图灵机 5. P 类与 NP 类语言 6. 多项式时间验证 7. 多项式时间变换 8. Cook定理 9. 合取范式的可满足性问题 CNF-SAT 10. 3 元合取范式的可满足性问题 3-SAT 11. 团问题 CLIQUE 12. 顶点覆盖问题 VERTEX-COVER 13. 子集和问题 SUBSET-SUM 14. 哈密顿回路问题 HAM-CYCLE 15. 旅行售货员问题 TSP 16. 顶点覆盖问题的近似算法 17. 旅行售货员问题近似算法 18. 具有三角不等式性质的旅行售货员问题 19. 一般的旅行售货员问题 20. 集合覆盖问题的近似算法 21. 子集和问题的近似算法 22. 子集和问题的指数时间算法 23. 子集和问题的多项式时间近似格式 |
| 位运算 | 位操作包括: 1. 取反(NOT) 2. 按位或(OR) 3. 按位异或(XOR) 4. 按位与(AND) 5. 移位: 是一个二元运算符,用来将一个二进制数中的每一位全部都向一个方向移动指定位,溢出的部分将被舍弃,而空缺的部分填入一定的值。 | 1.数字范围按位与 2.UTF-8 编码验证 3.数字转换为十六进制数 4.找出最长的超赞子字符串 5.数组异或操作 6.幂集 7.位1的个数 8.二进制表示中质数个计算置位 9.子数组异或查询 |
一. 时间复杂度数据规模 #
1s 内能解决问题的数据规模:10^6 ~ 10^7
- O(n^2) 算法可以处理 10^4 级别的数据规模(保守估计,处理 1000 级别的问题肯定没问题)
- O(n) 算法可以处理 10^8 级别的数据规模(保守估计,处理 10^7 级别的问题肯定没问题)
- O(nlog n) 算法可以处理 10^7 级别的数据规模(保守估计,处理 10^6 级别的问题肯定没问题)
| 数据规模 | 时间复杂度 | 算法举例 | |
|---|---|---|---|
| 1 | 10 | O(n!) | permutation 排列 |
| 2 | 20~30 | O(2^n) | combination 组合 |
| 3 | 50 | O(n^4) | DFS 搜索、DP 动态规划 |
| 4 | 100 | O(n^3) | 任意两点最短路径、DP 动态规划 |
| 5 | 1000 | O(n^2) | 稠密图、DP 动态规划 |
| 6 | 10^6 | O(nlog n) | 排序,堆,递归与分治 |
| 7 | 10^7 | O(n) | DP 动态规划、图遍历、拓扑排序、树遍历 |
| 8 | 10^9 | O(sqrt(n)) | 筛素数、求平方根 |
| 9 | 10^10 | O(log n) | 二分搜索 |
| 10 | +∞ | O(1) | 数学相关算法 |
| —————————— | —————————— | —————————————————————— | —————————————————————— |
一些具有迷惑性的例子:
void hello (int n){
for( int sz = 1 ; sz < n ; sz += sz )
for( int i = 1 ; i < n ; i ++ )
cout << "Hello" << endl;
}上面这段代码的时间复杂度是 O(nlog n) 而不是 O(n^2)
bool isPrime (int n){
for( int x = 2 ; x * x <= n ; x ++ )
if( n % x == 0 )
return false;
return true;
}上面这段代码的时间复杂度是 O(sqrt(n)) 而不是 O(n)。
再举一个例子,有一个字符串数组,将数组中的每一个字符串按照字母序排序,之后再将整个字符串数组按照字典序排序。两步操作的整体时间复杂度是多少呢?
如果回答是 O(n*nlog n + nlog n) = O(n^2log n),这个答案是错误的。字符串的长度和数组的长度是没有关系的,所以这两个变量应该单独计算。假设最长的字符串长度为 s,数组中有 n 个字符串。对每个字符串排序的时间复杂度是 O(slog s),将数组中每个字符串都按照字母序排序的时间复杂度是 O(n * slog s)。
将整个字符串数组按照字典序排序的时间复杂度是 O(s * nlog n)。排序算法中的 O(nlog n) 是比较的次数,由于比较的是整型数字,所以每次比较是 O(1)。但是字符串按照字典序比较,时间复杂度是 O(s)。所以字符串数组按照字典序排序的时间复杂度是 O(s * nlog n)。所以整体复杂度是 O(n * slog s) + O(s * nlog n) = O(nslog s + snlogn) = O(ns(log s + log n)) = O(nslog(n*s))。
二. 空间复杂度 #
递归调用是有空间代价的,递归算法需要保存递归栈信息,所以花费的空间复杂度会比非递归算法要高。
int sum( int n ){
assert( n >= 0 )
int ret = 0;
for ( int i = 0 ; i <= n ; i ++ )
ret += i;
return ret;
}上面算法的时间复杂度为 O(n),空间复杂度 O(1)。
int sum( int n ){
assert( n >= 0 )
if ( n == 0 )
return 0;
return n + sum( n - 1 );
}上面算法的时间复杂度为 O(n),空间复杂度 O(n)。
三. 递归的时间复杂度 #
1. 只有一次递归调用 #
如果递归函数中,只进行了一次递归调用,且递归深度为 depth,在每个递归函数中,时间复杂度为 T,那么总体的时间复杂度为 O(T * depth)
举个例子:
int binarySearch(int arr[], int l, int r, int target){
if( l > r )
return -1;
int mid = l + ( r - l ) / 2; // 防溢出
if(arr[mid] == target)
return mid;
else if (arr[mid] > target)
return binarySearch(arr,l,mid-1,target);
else
return binarySearch(arr,mid+1,r,target);
}在二分查找的递归实现中,只递归调用了自身。递归深度是 log n ,每次递归里面的复杂度是 O(1) 的,所以二分查找的递归实现的时间复杂度为 O(log n) 的。
2. 只有多次递归调用 #
针对多次递归调用的情况,就需要看它的计算调用的次数了。通常可以画一颗递归树来看。举例:
int f(int n){
assert( n >= 0 );
if( n == 0 )
return 1;
return f( n - 1 ) + f ( n - 1 );
}上述这次递归调用的次数为 2^0^ + 2^1^ + 2^2^ + …… + 2^n^ = 2^n+1^ - 1 = O(2^n)
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example 1:
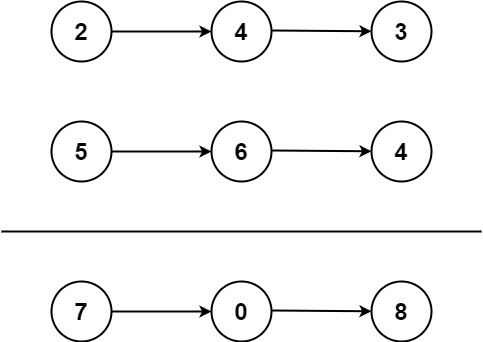
Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [7,0,8]
Explanation: 342 + 465 = 807.
Example 2:
Input: l1 = [0], l2 = [0]
Output: [0]
Example 3:
Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
Output: [8,9,9,9,0,0,0,1]
思路:
这个问题的解决方案实际上就是模拟了我们手动相加两个数的过程。首先,我们创建一个空链表来存储每一位的相加结果。在每一步中,我们将对应的节点值相加,并加上可能存在的进位(carry)。然后,我们将相加的结果对10取余数,这个余数就是新的节点的值。最后,我们通过将相加的结果除以10,得到的商就是下一步的进位。如果最后还有进位,我们会在链表的末尾添加一个新的节点
答案:
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
head := &ListNode{}
current , n1 ,n2 , carray := head, 0,0,0
for l1 != nil || l2 != nil || carray != nil{
if l1 == nil{
n1 = 0
}else{
n1 = l1.Val
l1 = l1.Next
}
if l2 == nil{
n2 = 0
}else{
n2 = l2.Val
l2 = l2.Next
}
current.Next = &ListNode{Val:(n1 + n2 +carray)%10}
carray := (n1 + n2 +carray) /10
}
return current.Next
}Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.
Return the head of the merged linked list.
解法一:
创建空的结果链表,然后每次比较l1 和l2 中的节点val大小,将结果指针节点指向结果较小的节点,当某个list为空的时候,将结果指针指向其余的节点
func mergeTwoList(l1 *ListNode, l2 *ListNode) *ListNode {
head := &ListNode{}
current := head
for l1 != nil && l2 != nil {
if l1.Val < l2.Val {
current.Next = l1
l1 = l1.Next
} else {
current.Next = l2
l2 = l2.Next
}
current = current.Next
}
if l1 == nil {
current.Next = l2
} else {
current.Next = l1
}
return head.Next
}解法二: 使用递归
func mergeTwoList(l1 *ListNode, l2 *ListNode) *ListNode {
if l1 == nil {
return l2
} else if l2 == nil {
return l1
} else if l1.Val < l2.Val {
l1.Next = mergeTwoList(l1.Next, l2)
return l1
} else {
l2.Next = mergeTwoList(l1, l2.Next)
return l2
}
}Given the root of a binary tree, return the inorder traversal of its nodes' values.
Example 1:
Input: root = [1,null,2,3]
Output: [1,3,2]
Example 2:
Input: root = []
Output: []
Example 3:
Input: root = [1]
Output: [1]
解法:
使用递归进行中序排序
func inorderTraversal(root *TreeNode) []int {
var result []int
inorder(root, &result)
return result
}
func inorder(root *TreeNode, output *[]int) {
if root != nil {
inorder(root.Left, output)
*output = append(*output, root.Val)
inorder(root.Right, output)
}
}