TSPg

The TSPg software implements the following algorithm that approximates Ward's agglomerative clustering:

Sieranoja, S., Fränti, P. Fast agglomerative clustering using approximate traveling salesman solutions. Journal of Big Data 12, 21 (2025). https://doi.org/10.1186/s40537-024-01053-x

The software is provided with GNU Lesser General Public License, Version 3. https://www.gnu.org/licenses/lgpl.html. All files except those under data and contrib -folders are subject to this license. See LICENSE.txt.

Contact: samisi@cs.uef.fi

Please, let me know how the software works for you if you try it out.

Python interface

Install & test

git clone https://github.com/uef-machine-learning/tspgclu.git
cd tspgclu
pip install -r requirements.txt
pip install .
python python/ex_cluster.py

Examples

See ex_* files in directory python/

Ward's agglomerative clustering using the TSP graph

(see file python/ex_cluster.py)

import numpy as np
import matplotlib.pyplot as plt

import tspg

def show_clusters_2d(x,labels,numclu):
	colormap = plt.cm.gist_ncar
	colorst = [colormap(i) for i in np.linspace(0, 0.9,numclu)]
	# print(colorst)
	u_labels = np.unique(labels)
	for i in u_labels:
		plt.scatter(x[labels == i , 0] , x[labels == i , 1] , label = i, color = colorst[i-1])
	plt.show()

# Fast version using built in distance functions written in C++:
def example_vec(ds,numclu):
	# For higher quality:
	#  - increase number of tsp paths (num_tsp), (in range [2,100])
	# Needs ds input in python list format
	labels,mergeOrder = tspg.tspg(ds.tolist(),numclu,distance="l2",num_tsp=5,dtype="vec")
	
	show_clusters_2d(ds,labels,numclu)

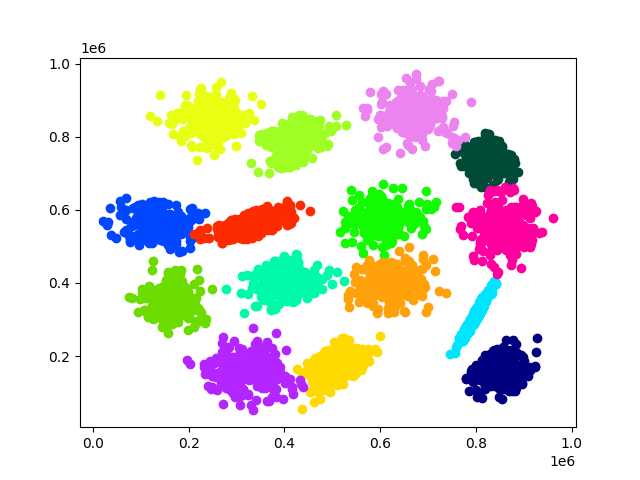
x=np.loadtxt('data/s1.txt')
example_vec(x,15)

Showing the dendogram

See python/ex_dendogram.py

...
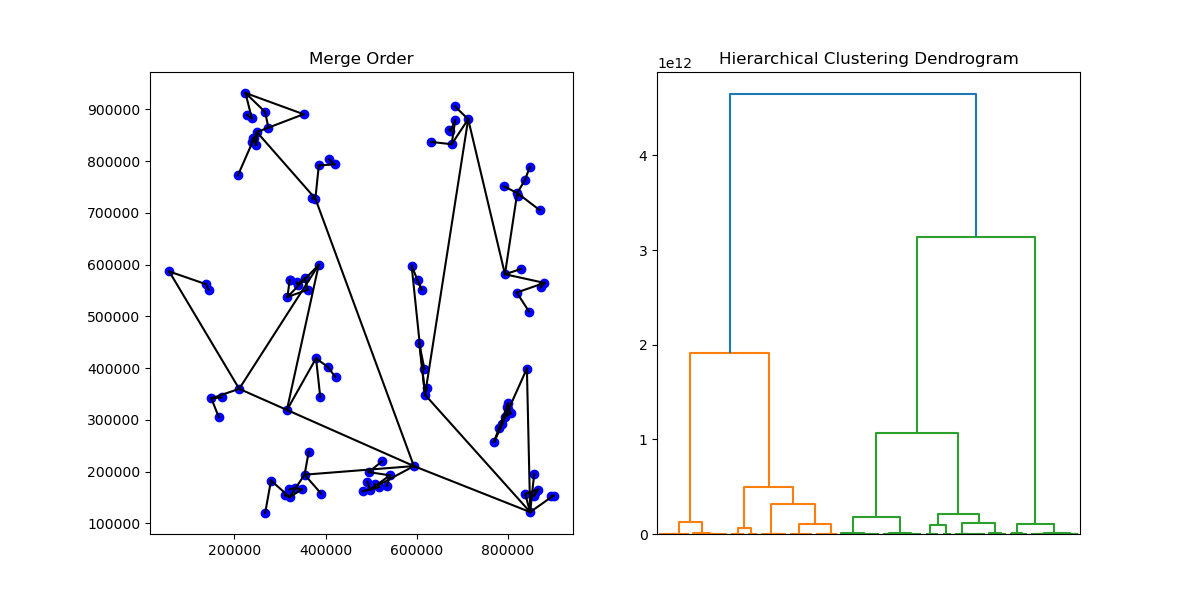
ds = np.genfromtxt('data/s1_small.txt')
labels,mergeOrder = tspg.tspg(ds.tolist(),1,distance="l2",num_tsp=5,dtype="vec")

mergeOrder_scipy = mergeOrderToScipyFormat(mergeOrder)

fig, axs = plt.subplots(1, 2, figsize=(12, 6), gridspec_kw={'width_ratios': [1, 1]})

plt1 = axs[0]; plt2 = axs[1]

# Create 2d plot showing the  merges
plt1.scatter(ds[:, 0], ds[:, 1], marker='o', color='b')
for pair in mergeOrder:
	plt1.plot([ds[pair[0],0], ds[pair[1],0]] , [ds[pair[0],1], ds[pair[1],1]], 'k-')
plt1.set_title('Merge Order')

# Plot the dendrogram
dendrogram(mergeOrder_scipy,ax=plt2,no_labels=True)
plt2.set_title('Hierarchical Clustering Dendrogram')
plt.show()

Getting the TSP graph

(file python/ex_create_graph.py)

import numpy as np
import matplotlib.pyplot as plt
import tspg
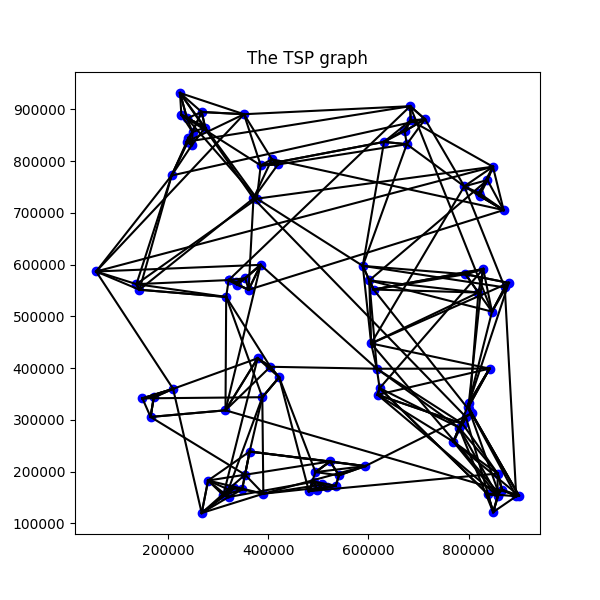
x=np.loadtxt('data/s1_small.txt')

# the graph is represented as num_tsp different linear orderings between the data x
paths = tspg.create_graph(x.tolist(),distance="l2",num_tsp=4)

plt.figure(figsize=(6, 6))
plt.scatter(x[:, 0], x[:, 1], marker='o', color='b')

for tsp in paths:
	for i in range(0,len(tsp)-1):
		# Draw line betwen consequtive points according the order in tsp  
		plt.plot([x[tsp[i],0], x[tsp[i+1],0]] , [x[tsp[i],1], x[tsp[i+1],1]], 'k-')

plt.title("The TSP graph")
plt.show()

Commandline interface

Compile

make clean
make

Use cases

Numerical (vectorial) data

Cluster vectorial (numerical) S1 dataset (data/s1.txt) to 15 clusters:

./tspg data/s1.txt --type vec -T 10  -C 15 --algo tspgclu -o tmp/s1part.txt  --cfn tmp/centroids.txt

For string data

./tspg  data/birkbeckU.txt --type txt -T 10 -C 20 --algo tspgclu --dfun lev -o tmp/birkbeckU_part.txt -H
./show_text_clusters.rb data/birkbeckU.txt tmp/birkbeckU_part.txt > tmp/text_clu.html